算法第四版 —— 快速排序
系列 - 算法第四版阅读笔记
目录
1 快速排序的优点
- 实现简单,适用于各种不同的输入数据,且在一般应用中比其他排序算法都要快的多;
- 原地排序,只需要很小的辅助栈的额外空间;
- 将长度为 N 的数组排序所需的时间和 N * lgN 成正比。
快速排序的缺点是非常脆弱,在实现时要非常小心才能避免低劣的性能。
2 快速排序基本算法
public class Quick {
/**
* Rearranges the array in ascending order, using the natural order.
*
* @param a the array to be sorted
*/
public static void sort(Comparable[] a) {
StdRandom.shuffle(a);
sort(a, 0, a.length - 1);
}
// quicksort the subarray from a[lo] to a[hi]
private static void sort(Comparable[] a, int lo, int hi) {
if (hi <= lo) return;
int j = partition(a, lo, hi);
sort(a, lo, j - 1);
sort(a, j + 1, hi);
}
// partition the subarray a[lo..hi] so that a[lo..j-1] <= a[j] <= a[j+1..hi]
// and return the index j.
private static int partition(Comparable[] a, int lo, int hi) {
int i = lo;
int j = hi + 1;
Comparable v = a[lo];
while (true) {
// find item on lo to swap
while (less(a[++i], v)) {
if (i == hi) break;
}
// find item on hi to swap
while (less(v, a[--j])) {
if (j == lo) break; // redundant since a[lo] acts as sentinel
}
// check if pointers cross
if (i >= j) break;
exch(a, i, j);
}
// put partitioning item v at a[j]
exch(a, lo, j);
// now, a[lo .. j-1] <= a[j] <= a[j+1 .. hi]
return j;
}
// is v < w ?
private static boolean less(Comparable v, Comparable w) {
if (v == w) return false; // optimization when reference equals
return v.compareTo(w) < 0;
}
// exchange a[i] and a[j]
private static void exch(Object[] a, int i, int j) {
Object swap = a[i];
a[i] = a[j];
a[j] = swap;
}
}快速排序是一种分治的排序算法。它将一个数组切分成两个子数组,将两部分独立地排序。其与归并排序是互补的。
由于切分过程总是能排定一个元素,用归纳法可以证明递归能够正确地将数组排序:如果左子数组和右子数组都是有序的,那么由左子数组、切分元素和右子数组组成的结果数组也一定是有序的。
3 快速排序的性能特点
由于快速排序切分方法的内循环简洁短小,相比归并排序与希尔排序,其内循环中很少移动数据,因此快速排序性能一般比其他的排序算法性能高。
快速排序的另一个特点是比较次数很少,快速排序的最好情况是每次都正好能将数组对半分。
4 快速排序的算法改进
- 切换到插入排序。对于小数组,快速排序比插入排序慢。因为快速排序的 sort 递归方法在小数组中也会调用自己。
- 三取样切分。能够使得快速排序的切分效果更好,但代价是需要计算中位数。同时可以将取样元素放在数组末尾作为“哨兵”来去掉切分方法的边界测试。
- 熵最优排序。一个元素全部重复的子数组不需要继续排序,但是快速排序的基础算法还会继续将它切分为更小的数组。在含有大量重复元素的数组的情况下,快速排序会使元素全部重复的子数组经常出现,这部分的优化能够将当前线性对数级的性能提高到线性级别。
4.1 快速排序的哨兵
public class QuickSentinel {
public static void sort(Comparable[] a) {
if (a == null || a.length < 2) return;
// 将数组的最大元素放在最右边作为哨兵,除非和相等的元素交换,否则该元素永远不会移动
int maxIndex = 0;
for (int i = 1; i < a.length; i++) {
if (less(a[maxIndex], a[i])) {
maxIndex = i;
}
}
exch(a, maxIndex, a.length - 1);
sort(a, 0, a.length - 1);
}
private static void sort(Comparable[] a, int lo, int hi) {
if (lo >= hi) return;
int mid = partition(a, lo, hi);
sort(a, lo, mid - 1);
sort(a, mid + 1, hi);
}
private static int partition(Comparable[] a, int lo, int hi) {
int i = lo, j = hi + 1;
Comparable pivot = a[lo];
while (true) {
while (less(a[++i], pivot)) { // 切分元素本身就是哨兵
}
while (less(pivot, a[--j])) { // 右侧哨兵取消边界检查
}
if (i >= j) break;
exch(a, i, j);
}
exch(a, lo, j);
return j;
}
}4.2 快速排序的非递归实现
class QuickNoRecursive {
public static void sort(Comparable[] a) {
if (a == null || a.length < 2) return;
Stack<Integer> stack = new Stack<>();
stack.push(0);
stack.push(a.length - 1);
sort(a, stack);
}
// 使用栈来模拟递归栈
private static void sort(Comparable[] a, Stack<Integer> stack) {
while (!stack.isEmpty()) {
int hi = stack.pop();
int lo = stack.pop();
if (lo >= hi) continue;
int mid = partition(a, lo, hi);
// 先将较小的子数组压入栈,可以保证栈最多只会有 lgN 个元素
if (hi - mid > mid - lo) {
stack.push(mid + 1);
stack.push(hi);
stack.push(lo);
stack.push(mid - 1);
} else {
stack.push(lo);
stack.push(mid - 1);
stack.push(mid + 1);
stack.push(hi);
}
}
}
private static int partition(Comparable[] a, int lo, int hi) {
int i = lo;
int j = hi + 1;
Comparable v = a[lo];
while (true) {
while (less(a[++i], v)) {
if (i == hi) break;
}
while (less(v, a[--j])) {
if (j == lo) break;
}
if (i >= j) break;
exch(a, i, j);
}
exch(a, lo, j);
return j;
}
}4.3 快速排序优化代码的实现
public class Quick {
// cutoff to insertion sort, must be >= 1
private static final int INSERTION_SORT_CUTOFF = 8;
/**
* Rearranges the array in ascending order, using the natural order.
* @param a the array to be sorted
*/
public static void sort(Comparable[] a) {
// StdRandom.shuffle(a);
sort(a, 0, a.length - 1);
}
// quicksort the subarray from a[lo] to a[hi]
private static void sort(Comparable[] a, int lo, int hi) {
if (hi <= lo) return;
// cutoff to insertion sort (Insertion.sort() uses half-open intervals)
int n = hi - lo + 1;
if (n <= INSERTION_SORT_CUTOFF) {
Insertion.sort(a, lo, hi + 1);
return;
}
int j = partition(a, lo, hi);
sort(a, lo, j-1);
sort(a, j+1, hi);
}
// partition the subarray a[lo..hi] so that a[lo..j-1] <= a[j] <= a[j+1..hi]
// and return the index j.
private static int partition(Comparable[] a, int lo, int hi) {
int n = hi - lo + 1;
int m = median3(a, lo, lo + n/2, hi); // 取样确定切分元素
exch(a, m, lo);
int i = lo;
int j = hi + 1;
Comparable v = a[lo];
// 切分元素为最大、最小的情况,直接返回
// a[lo] is unique largest element
while (less(a[++i], v)) {
if (i == hi) { exch(a, lo, hi); return hi; }
}
// a[lo] is unique smallest element
while (less(v, a[--j])) {
if (j == lo + 1) return lo;
}
// the main loop
while (i < j) {
exch(a, i, j);
while (less(a[++i], v)) ;
while (less(v, a[--j])) ;
}
// put partitioning item v at a[j]
exch(a, lo, j);
// now, a[lo .. j-1] <= a[j] <= a[j+1 .. hi]
return j;
}
// return the index of the median element among a[i], a[j], and a[k]
private static int median3(Comparable[] a, int i, int j, int k) {
return (less(a[i], a[j]) ?
(less(a[j], a[k]) ? j : less(a[i], a[k]) ? k : i) :
(less(a[k], a[j]) ? j : less(a[k], a[i]) ? k : i));
}
// is v < w ?
private static boolean less(Comparable v, Comparable w) {
return v.compareTo(w) < 0;
}
// exchange a[i] and a[j]
private static void exch(Object[] a, int i, int j) {
Object swap = a[i];
a[i] = a[j];
a[j] = swap;
}
}上述代码是对二向切分的快速排序的优化版本:
- 每次排序抽样三个元素,并以三个元素的中位数作为切分元素,优化切分效果;
- 使用插入排序提升小数组的排序速度;
- 对于切分元素 lo 是最大(最小)情况进行优化。
5 三向切分的快速排序
三向切分的快速排序适用于大量重复主键的随机数组。通过统计待排序数组的香农信息量,可以得出三向切分的快速排序所需要的比较次数的上下界。
三向切分的快速排序是信息量最优的。因为对于包含大量重复元素的数组,它将排序时间从线性对数级降低到了线性级别。三向切分的最坏情况正是所有主键均不相同。
5.1 Dijkstra 三向切分的快速排序
public class Quick3way {
/**
* Rearranges the array in ascending order, using the natural order.
*
* @param a the array to be sorted
*/
public static void sort(Comparable[] a) {
StdRandom.shuffle(a);
sort(a, 0, a.length - 1);
}
// quicksort the subarray a[lo .. hi] using 3-way partitioning
private static void sort(Comparable[] a, int lo, int hi) {
if (hi <= lo) return;
int lt = lo, gt = hi;
Comparable v = a[lo];
int i = lo + 1;
while (i <= gt) { // 从左到右遍历数组一次
int cmp = a[i].compareTo(v); // 使用 compareTo 比较元素,而非 less 方法
if (cmp < 0) exch(a, lt++, i++);
else if (cmp > 0) exch(a, i, gt--);
else i++;
}
// a[lo..lt-1] < v = a[lt..gt] < a[gt+1..hi].
sort(a, lo, lt - 1);
sort(a, gt + 1, hi);
}
}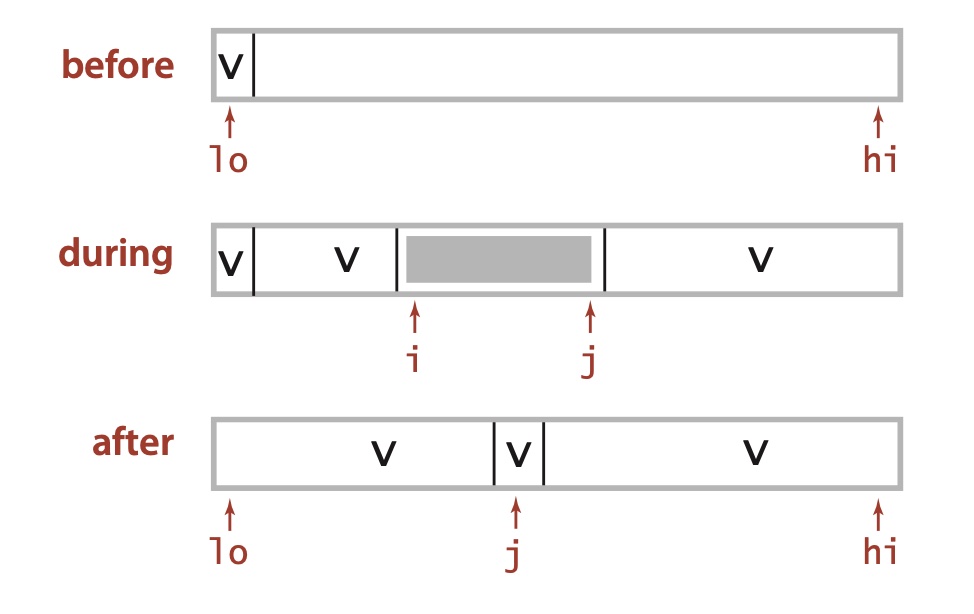
从左到右遍历数组一次,维护一个指针 lt 使得 a[lo..lt-1] 中的元素都小于 v,一个指针 gt 使得 a[gt+1..hi] 中的元素都大于 v,,一个指针 i 使得 a[lt..i-1] 中的元素都等于 v,a[i..gt] 中的元素都还未确定。
- a[i] 小于 v,将 a[lt] 和 a[i] 交换,将 lt 和 i 加一;
- a[i] 大于 v,将 a[gt] 和 a[i] 交换,将 gt 减一;
- a[j] 等于 v,将 i 加一。
在数组中重复元素不多的普通情况下它比标准的二分法多使用了很多次交换。J.Bently 和 D.Mcllrov 的快速排序方法,使得三向切分的快速排序比归并排序和其他排序方法在包括重复元素很多的实际应用中更快。
5.2 快速三向切分(J.Bently, D.Mcllrov)
public class QuickBentleyMcIlroy {
// cutoff to insertion sort, must be >= 1
private static final int INSERTION_SORT_CUTOFF = 8;
// cutoff to median-of-3 partitioning
private static final int MEDIAN_OF_3_CUTOFF = 40;
/**
* Rearranges the array in ascending order, using the natural order.
* @param a the array to be sorted
*/
public static void sort(Comparable[] a) {
sort(a, 0, a.length - 1);
}
private static void sort(Comparable[] a, int lo, int hi) {
int n = hi - lo + 1;
// cutoff to insertion sort
if (n <= INSERTION_SORT_CUTOFF) {
insertionSort(a, lo, hi);
return;
}
// use median-of-3 as partitioning element
else if (n <= MEDIAN_OF_3_CUTOFF) {
int m = median3(a, lo, lo + n/2, hi);
exch(a, m, lo);
}
// use Tukey ninther as partitioning element
else {
int eps = n/8;
int mid = lo + n/2;
int m1 = median3(a, lo, lo + eps, lo + eps + eps);
int m2 = median3(a, mid - eps, mid, mid + eps);
int m3 = median3(a, hi - eps - eps, hi - eps, hi);
int ninther = median3(a, m1, m2, m3);
exch(a, ninther, lo);
}
// Bentley-McIlroy 3-way partitioning
int i = lo, j = hi+1;
int p = lo, q = hi+1;
Comparable v = a[lo];
while (true) {
while (less(a[++i], v))
if (i == hi) break;
while (less(v, a[--j]))
if (j == lo) break;
// pointers cross
if (i == j && eq(a[i], v))
exch(a, ++p, i);
if (i >= j) break;
exch(a, i, j);
if (eq(a[i], v)) exch(a, ++p, i);
if (eq(a[j], v)) exch(a, --q, j);
}
i = j + 1;
for (int k = lo; k <= p; k++)
exch(a, k, j--);
for (int k = hi; k >= q; k--)
exch(a, k, i++);
sort(a, lo, j);
sort(a, i, hi);
}
// sort from a[lo] to a[hi] using insertion sort
private static void insertionSort(Comparable[] a, int lo, int hi) {
for (int i = lo; i <= hi; i++)
for (int j = i; j > lo && less(a[j], a[j-1]); j--)
exch(a, j, j-1);
}
// return the index of the median element among a[i], a[j], and a[k]
private static int median3(Comparable[] a, int i, int j, int k) {
return (less(a[i], a[j]) ?
(less(a[j], a[k]) ? j : less(a[i], a[k]) ? k : i) :
(less(a[k], a[j]) ? j : less(a[k], a[i]) ? k : i));
}
// is v < w ?
private static boolean less(Comparable v, Comparable w) {
if (v == w) return false; // optimization when reference equal
return v.compareTo(w) < 0;
}
// does v == w ?
private static boolean eq(Comparable v, Comparable w) {
if (v == w) return true; // optimization when reference equal
return v.compareTo(w) == 0;
}
// exchange a[i] and a[j]
private static void exch(Object[] a, int i, int j) {
Object swap = a[i];
a[i] = a[j];
a[j] = swap;
}
}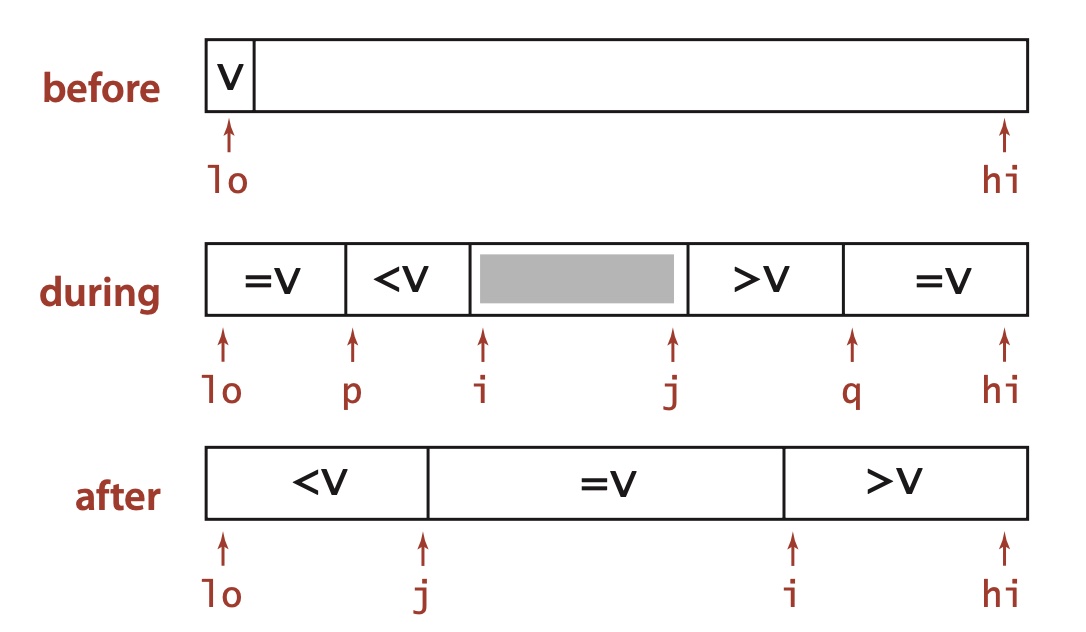
上述代码的基本思想是:将重复元素放置于子数组两端的方式实现的信息量最优的排序算法。
- 使用两个索引 p 和 q,使得 a[lo..p-1] 和 a[q+1..hi] 的元素都和 a[lo] 相等。
- 使用另外两个索引 i 和 j,使得 a[p..i-1] 小于 a[lo],a[j+i..q]大于 a[lo]。
- 在内循环中加入代码,在 a[i] 和 v 相当时将其与 a[p] 交换(并将 p 加 1 ),在 a[j] 和 v 相等且 a[i] 和 a[j] 尚未和 v 进行比较之前将其与 a[q] 交换。
- 使用 Tukey’s ninther 方法来找出切分元素,选择三组,每组三个元素,分别取三组元素的中位数,然后取三个中位数的中位数作为切分元素,且在排序小数组时切换到插入排序。