算法第四版 —— 优先队列
1 基本优先队列
1.1 优先队列 API
优先队列最重要的操作是删除最大元素和插入元素。
泛型优先队列的 API
public class MaxPQ<Key extends Comparable<Key>>
MaxPQ() 创建一个优先队列
MaxPQ(int max) 创建一个初始容量为 max 的优先队列
MaxPQ(Key a) 用 a[] 中的元素创建一个优先队列
void insert(Key v) 向优先队列中插入一个元素
Key max() 返回最大元素
Key delMax() 删除并返回最大元素
boolean isEmpty() 返回队列是否为空
int size() 返回优先队列中的元素个数1.2 优先队列的基本实现
数据结构二叉堆能够很好地实现优先队列的基本操作。
1.2.1 堆的定义与表示
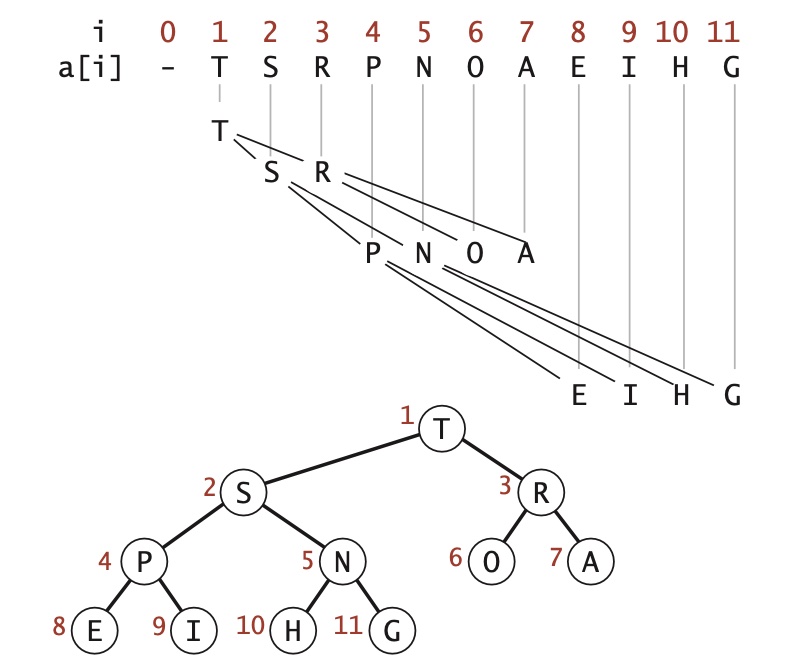
二叉堆:一组能够用堆有序的完全二叉树排序的元素,并在数组中按照层级存储(不使用数组的第一个位置)。
堆有序:当一颗二叉树的每个结点都大于等于它的两个子结点时,它被称为堆有序。
1.2.2 堆的算法
优先队列由一个基于堆的完全二叉树表示,存储于数组 pq[1..N] 中,pq[0] 没有使用。
在 insert 中,将 n 加一并把新元素添加在数组最后,然后用 swim 保证堆有序。
在 delMax 中,从 pq[1] 中得到需要返回的元素,然后将 pq[N] 移动到 pq[1],将 N 减一并用 sink 保证堆有序。
public class MaxPQ<Key extends Comparable<Key>> {
private Key[] pq; // store items at indices 1 to n
private int n; // number of items on priority queue
public MaxPQ() {
this(1);
}
public MaxPQ(int initCapacity) {
pq = (Key[]) new Object[initCapacity + 1];
n = 0;
}
public MaxPQ(Key[] keys) {
n = keys.length;
pq = (Key[]) new Object[keys.length + 1];
for (int i = 0; i < n; i++)
pq[i + 1] = keys[i];
for (int k = n / 2; k >= 1; k--)
sink(k);
}
public void insert(Key x) {
// double size of array if necessary
if (n == pq.length - 1) resize(2 * pq.length);
// add x, and percolate it up to maintain heap invariant
pq[++n] = x;
swim(n);
}
public Key max() {
if (isEmpty()) throw new NoSuchElementException("Priority queue underflow");
return pq[1];
}
public Key delMax() {
if (isEmpty()) throw new NoSuchElementException("Priority queue underflow");
Key max = pq[1];
exch(1, n--);
sink(1);
pq[n + 1] = null; // to avoid loitering and help with garbage collection
if ((n > 0) && (n == (pq.length - 1) / 4)) resize(pq.length / 2);
return max;
}
public boolean isEmpty() {
return n == 0;
}
public int size() {
return n;
}
private void resize(int capacity) {
assert capacity > n;
Key[] temp = (Key[]) new Object[capacity];
for (int i = 1; i <= n; i++) {
temp[i] = pq[i];
}
pq = temp;
}
/***************************************************************************
* Helper functions to restore the heap invariant.
***************************************************************************/
private void swim(int k) {
while (k > 1 && less(k / 2, k)) {
exch(k / 2, k);
k = k / 2;
}
}
private void sink(int k) {
while (2 * k <= n) {
int j = 2 * k;
if (j < n && less(j, j + 1)) j++;
if (!less(k, j)) break;
exch(k, j);
k = j;
}
}
/***************************************************************************
* Helper functions for compares and swaps.
***************************************************************************/
private boolean less(int v, int w) {
return pq[v].compareTo(pq[w]) < 0;
}
private void exch(int v, int w) {
Key swap = pq[v];
pq[v] = pq[w];
pq[w] = swap;
}
}1.3 优先队列的应用
一个基本的优先队列应用是在庞大的输入中找出最大(最小)的元素。
public class TopM {
public static void main(String[] args) {
int m = Integer.parseInt(args[0]);
MinPQ<Transaction> pq = new MinPQ<>(m + 1);
while (StdIn.hasNextLine()) {
// Create an entry from the next line and put on the PQ.
String line = StdIn.readLine();
Transaction transaction = new Transaction(line);
pq.insert(transaction);
// remove minimum if m+1 entries on the PQ
if (pq.size() > m)
pq.delMin();
} // top m entries are on the PQ
// print entries on PQ in reverse order
Stack<Transaction> stack = new Stack<>();
for (Transaction transaction : pq)
stack.push(transaction);
for (Transaction transaction : stack)
StdOut.println(transaction);
}
}2 索引优先队列
在很多应用中,允许用例引用已经进入优先队列中的元素是有必要的(允许用例访问在优先队列中的任意元素)。
理解这种数据结构的一个方法是:将它看成一个能够快速访问其中最小元素的数组。
2.1 索引优先队列 API
泛型优先队列的 API
public class IndexMinPQ<Item extends Comparable<Item>>
IndexMinPQ(int maxN) 创建一个最大容量为 maxN 的优先队列
索引的取值范围为 0 至 maxN - 1
void insert(int k, Item item) 插入一个元素,将它和索引 k 相关联
void change(int k, Item item) 将索引 k 的元素设为 item
boolean contains(int k) 是否存在索引为 k 的元素
void delete(int k) 删去索引 k 及其相关联的元素
Item min() 返回最小元素
int minIndex() 返回最小元素的索引
int delMin() 删除最小元素并返回它的索引
boolean isEmpty() 返回队列是否为空
int size() 返回优先队列中的元素个数2.2 索引优先队列的实现
public class IndexMinPQ<Key extends Comparable<Key>> {
/**
* keys: 所有元素存储在 keys 数组中,并与索引进行绑定
* pq : 索引二叉堆
* qp : 存储索引的索引,qp[i] 表示 keys[i] 元素对应的索引在 pq 的位置(索引)
* 即对于索引为 i 的元素 pq[qp[i]] = i
*
* 为什么需要记录元素索引的索引?
* 在 deleteMin / changeKey 方法中变更任意元素 keys[i]
* 可以直接通过 qp[i] 获取索引在二叉堆 pq 中的位置(索引的索引)
*/
private int maxN; // maximum number of elements on PQ
private int n; // number of elements on PQ
private int[] pq; // binary heap using 1-based indexing
private int[] qp; // inverse of pq - qp[pq[i]] = pq[qp[i]] = i
private Key[] keys; // keys[i] = priority of i
public IndexMinPQ(int maxN) {
if (maxN < 0) throw new IllegalArgumentException();
this.maxN = maxN;
n = 0;
keys = (Key[]) new Comparable[maxN + 1];
pq = new int[maxN + 1];
qp = new int[maxN + 1];
for (int i = 0; i <= maxN; i++)
qp[i] = -1;
}
public void insert(int i, Key key) {
validateIndex(i);
if (contains(i)) throw new IllegalArgumentException("index is already in the priority queue");
keys[i] = key;
n++;
pq[n] = i; // 将索引 i 加入到 pq[] 最后
qp[i] = n;
swim(n);
}
public void changeKey(int i, Key key) {
validateIndex(i);
if (!contains(i)) throw new NoSuchElementException("index is not in the priority queue");
keys[i] = key;
swim(qp[i]);
sink(qp[i]);
}
public boolean contains(int i) {
validateIndex(i);
return qp[i] != -1;
}
public void delete(int i) {
validateIndex(i);
if (!contains(i)) throw new NoSuchElementException("index is not in the priority queue");
int index = qp[i];
exch(index, n--);
swim(index);
sink(index);
keys[i] = null;
qp[i] = -1;
}
public Key minKey() {
if (n == 0) throw new NoSuchElementException("Priority queue underflow");
return keys[pq[1]];
}
public int minIndex() {
if (n == 0) throw new NoSuchElementException("Priority queue underflow");
return pq[1];
}
public int delMin() {
if (n == 0) throw new NoSuchElementException("Priority queue underflow");
int min = pq[1];
exch(1, n--);
sink(1);
assert min == pq[n + 1];
qp[min] = -1; // delete
keys[min] = null; // to help with garbage collection
pq[n + 1] = -1; // not needed
return min;
}
public Key keyOf(int i) {
validateIndex(i);
if (!contains(i))
throw new NoSuchElementException("index is not in the priority queue");
return keys[i];
}
public boolean isEmpty() {
return n == 0;
}
public int size() {
return n;
}
private void validateIndex(int i) {
if (i < 0) throw new IllegalArgumentException("index is negative: " + i);
if (i >= maxN) throw new IllegalArgumentException("index >= capacity: " + i);
}
/***************************************************************************
* Heap helper functions.
***************************************************************************/
private void swim(int k) {
while (k > 1 && greater(k / 2, k)) {
exch(k, k / 2);
k = k / 2;
}
}
private void sink(int k) {
while (2 * k <= n) {
int j = 2 * k;
if (j < n && greater(j, j + 1)) j++;
if (!greater(k, j)) break;
exch(k, j);
k = j;
}
}
/***************************************************************************
* General helper functions.
***************************************************************************/
private boolean greater(int v, int w) {
return keys[pq[v]].compareTo(keys[pq[w]]) > 0;
}
private void exch(int v, int w) {
int swap = pq[v];
pq[v] = pq[w];
pq[w] = swap;
// 索引 pq[v] 与 pq[w] 交换,此时 pq[v] 指向 keys[w], pq[w] 指向 keys[v]
qp[pq[v]] = v;
qp[pq[w]] = w;
}
}2.3 索引优先队列用例
多向归并问题:将多个有序的输入流归并成一个有序的输出流。
使用优先队列解决多向归并问题,无论输入有多长都可以将其全部读入并排序。
public class Multiway {
public static void merge(In[] streams) {
// 每个输入流对应索引优先队列的一个索引
int N = streams.length;
IndexMinPQ<String> pq = new IndexMinPQ<>(N);
// 每个输入流的索引都关联一个元素(输入中的下一个字符串)
for (int i = 0; i < N; i++)
if (!streams[i].isEmpty())
pq.insert(i, streams[i].readString());
// 删除并打印出队列中最小字符串
// 然后将该输入的下一个字符串添加到优先队列
while (!pq.isEmpty()) {
StdOut.println(pq.min());
int i = pq.delMin();
if (!streams[i].isEmpty())
pq.insert(i, streams[i].readString());
}
}
public static void main(String[] args) {
int N = args.length;
In[] streams = new In[N];
for (int i = 0; i < N; i++)
streams[i] = new In(args[i]);
merge(streams);
}
}3 堆排序
堆排序算法:堆排序算法分为两个阶段,堆的构造阶段和下沉排序阶段。
在堆的构造阶段,我们将原始数组重新组织安排进一个堆中。
在下沉排序阶段,我们从堆中按递减顺序取出所有元素并得到排序结果。
3.1 堆的构造
构造堆的一个高效方法是使用 sink 方法从右至左构造子堆。如果一个结点的两个子结点已经是堆了,那么在该结点上调用 sink 方法可以将它们变成一个堆。
开始时我们只需要扫描数组中的一半元素,因为我们可以提哦啊过大小为 1 的子堆。最后我们在位置 1 上调用 sink 方法,堆构造结束。
3.2 下沉排序
我们将堆中的最大元素删除,然后放入堆缩小后数组中空出的位置,直至销毁堆,下沉排序完成。
public class Heap {
public static void sort(Comparable[] pq) {
int n = pq.length;
// heapify phase
for (int k = n/2; k >= 1; k--)
sink(pq, k, n);
// sortdown phase
int k = n;
while (k > 1) {
exch(pq, 1, k--);
sink(pq, 1, k);
}
}
}3.3 先下沉后上浮(Floyd 优化)
大多数在下沉排序期间重新插入堆的元素会下沉到堆底。
通过先下沉后上浮,我们正好可以通过免去检查元素是否到达正确的位置来节省时间。在下沉过程中总是直接提升较大的子结点直至到达堆底。然后再使元素上浮到正确的位置。
这种方法可以将比较次数减少一半,接近归并排序所需的比较次数。
public class FloydHeap {
public static void sort(Comparable[] pq) {
int n = pq.length;
// heapify phase
for (int k = n / 2; k >= 1; k--)
sink(pq, k, n);
// sortdown phase
int k = n;
while (k > 1) {
exch(pq, 1, k--);
sinkThenSwim(pq, 1, k);
}
}
private static void sink(Comparable[] pq, int k, int n) {
while (2 * k <= n) {
int j = 2 * k;
if (j < n && less(pq, j, j + 1)) j++;
if (!less(pq, k, j)) break;
exch(pq, k, j);
k = j;
}
}
private static void swim(Comparable[] pq, int k) {
while (k > 1 && less(pq, k / 2, k)) {
exch(pq, k, k / 2);
k /= 2;
}
}
private static void sinkThenSwim(Comparable[] pq, int k, int n) {
while (2 * k <= n) {
int j = 2 * k;
if (j < n && less(pq, j, j + 1)) j++;
// 免去检查元素是否到达正确位置
// if (!less(pq, k, j)) break;
exch(pq, k, j);
k = j;
}
// swim 到正确位置
swim(pq, k);
}
}