算法第四版 —— 二叉查找树
一棵二叉查找树(BST)是一棵二又树,其中每个结点都含有一个 Comparable 的键(以及相关联的值)且每个结点的键都大于其左子树中的任意结点的键而小于右子树的任意结点的键。
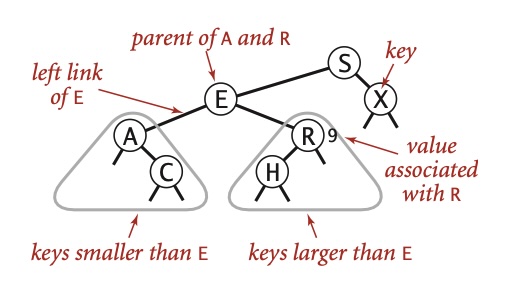
1 基本实现
public class BST<Key extends Comparable<Key>, Value> {
private Node root; // root of BST
private class Node {
private Key key; // sorted by key
private Value val; // associated data
private Node left, right; // left and right subtrees
private int size; // number of nodes in subtree
public Node(Key key, Value val, int size) {
this.key = key;
this.val = val;
this.size = size;
}
}
/**
* Initializes an empty symbol table.
*/
public BST() {
}
/**
* Returns the number of key-value pairs in this symbol table.
* @return the number of key-value pairs in this symbol table
*/
public int size() {
return size(root);
}
// return number of key-value pairs in BST rooted at x
private int size(Node x) {
if (x == null) return 0;
else return x.size;
}
}1.1 查找(get)
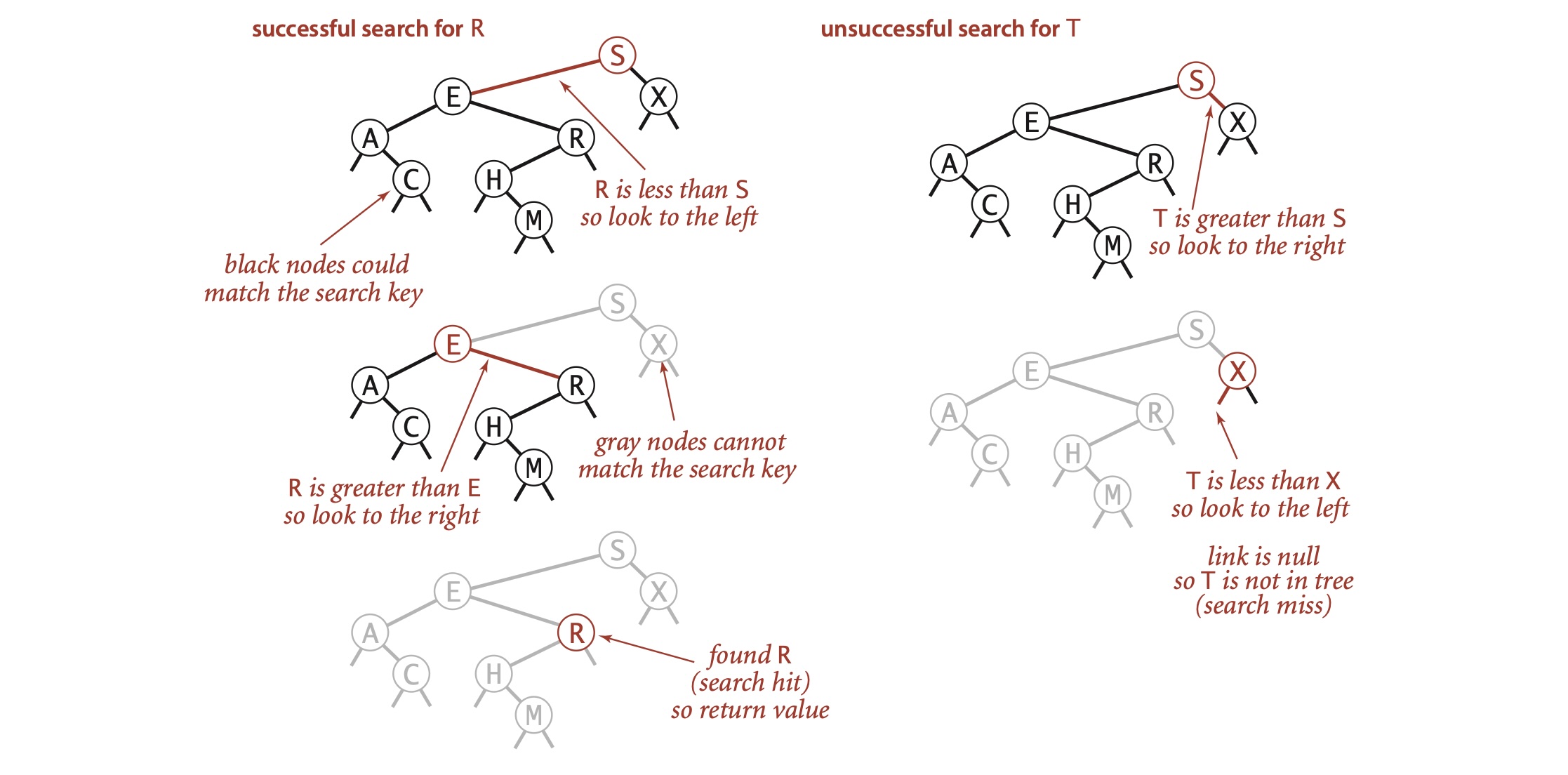
查找结点流程:如果树是空的,则查找未命中;如果查找的键和根结点的键相等,查找命中;否则递归地在子树中查找。如果被查找的键较小就选择左子树,较大则选择右子树。
public class BST<Key extends Comparable<Key>, Value> {
/**
* Returns the value associated with the given key.
*
* @param key the key
* @return the value associated with the given key if the key is in the symbol table
* and {@code null} if the key is not in the symbol table
* @throws IllegalArgumentException if {@code key} is {@code null}
*/
public Value get(Key key) {
return get(root, key);
}
private Value get(Node x, Key key) {
if (key == null)
throw new IllegalArgumentException("calls get() with a null key");
if (x == null) return null;
int cmp = key.compareTo(x.key);
if (cmp < 0) return get(x.left, key);
else if (cmp > 0) return get(x.right, key);
else return x.val;
}
}1.2 插入(put)
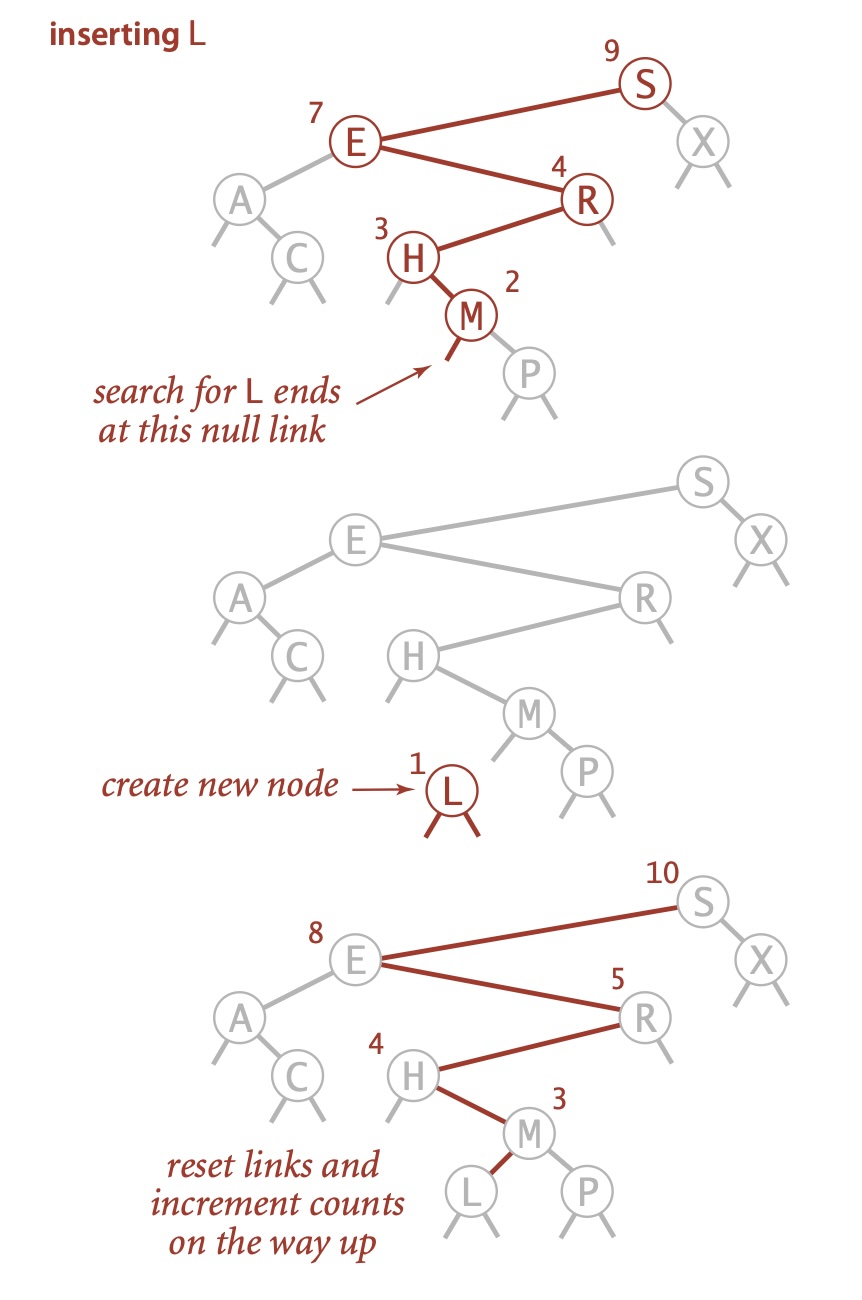
插入结点流程:如果树是空的,就返回一个含有该键值对的新结点;如果被查找的键小于根结点的键,就在左子树中插入该键,否则在右子树插入该键。
public class BST<Key extends Comparable<Key>, Value> {
/**
* Inserts the specified key-value pair into the symbol table, overwriting the old
* value with the new value if the symbol table already contains the specified key.
* Deletes the specified key (and its associated value) from this symbol table
* if the specified value is {@code null}.
*
* @param key the key
* @param val the value
* @throws IllegalArgumentException if {@code key} is {@code null}
*/
public void put(Key key, Value val) {
if (key == null)
throw new IllegalArgumentException("calls put() with a null key");
if (val == null) {
delete(key);
return;
}
root = put(root, key, val);
assert check();
}
private Node put(Node x, Key key, Value val) {
if (x == null)
return new Node(key, val, 1);
int cmp = key.compareTo(x.key);
if (cmp < 0) x.left = put(x.left, key, val);
else if (cmp > 0) x.right = put(x.right, key, val);
else x.val = val;
x.size = 1 + size(x.left) + size(x.right);
return x;
}
}可以将递归调用前的代码想象成沿着树向下走:它会将给定的键和每个结点的键相比较并根据结果向左或者向右移动到下一个结点。
可以将递归调用后的代码想象成沿着树向上爬:对于 get() 方法对应着一系列的返回指令,对于 put() 方法意味着重置搜索路径上每一个父结点指向子结点的链接,并增加路径上每个结点中的计数器的值。
2 有序性相关的方法与删除操作
2.1 最大键和最小键(max / min)
如果根结点的左链接为空,那么一棵二叉查找树中最小的键就是根结点;如果左链接非空,那么树中的最小键就是左子树中的最小键。
public class BST<Key extends Comparable<Key>, Value> {
/**
* Returns the smallest key in the symbol table.
*
* @return the smallest key in the symbol table
* @throws NoSuchElementException if the symbol table is empty
*/
public Key min() {
if (isEmpty())
throw new NoSuchElementException("calls min() with empty symbol table");
return min(root).key;
}
private Node min(Node x) {
if (x.left == null) return x;
else return min(x.left);
}
/**
* Returns the largest key in the symbol table.
*
* @return the largest key in the symbol table
* @throws NoSuchElementException if the symbol table is empty
*/
public Key max() {
if (isEmpty())
throw new NoSuchElementException("calls max() with empty symbol table");
return max(root).key;
}
private Node max(Node x) {
if (x.right == null) return x;
else return max(x.right);
}
}2.2 向上取整和向下取整(floor / ceiling)
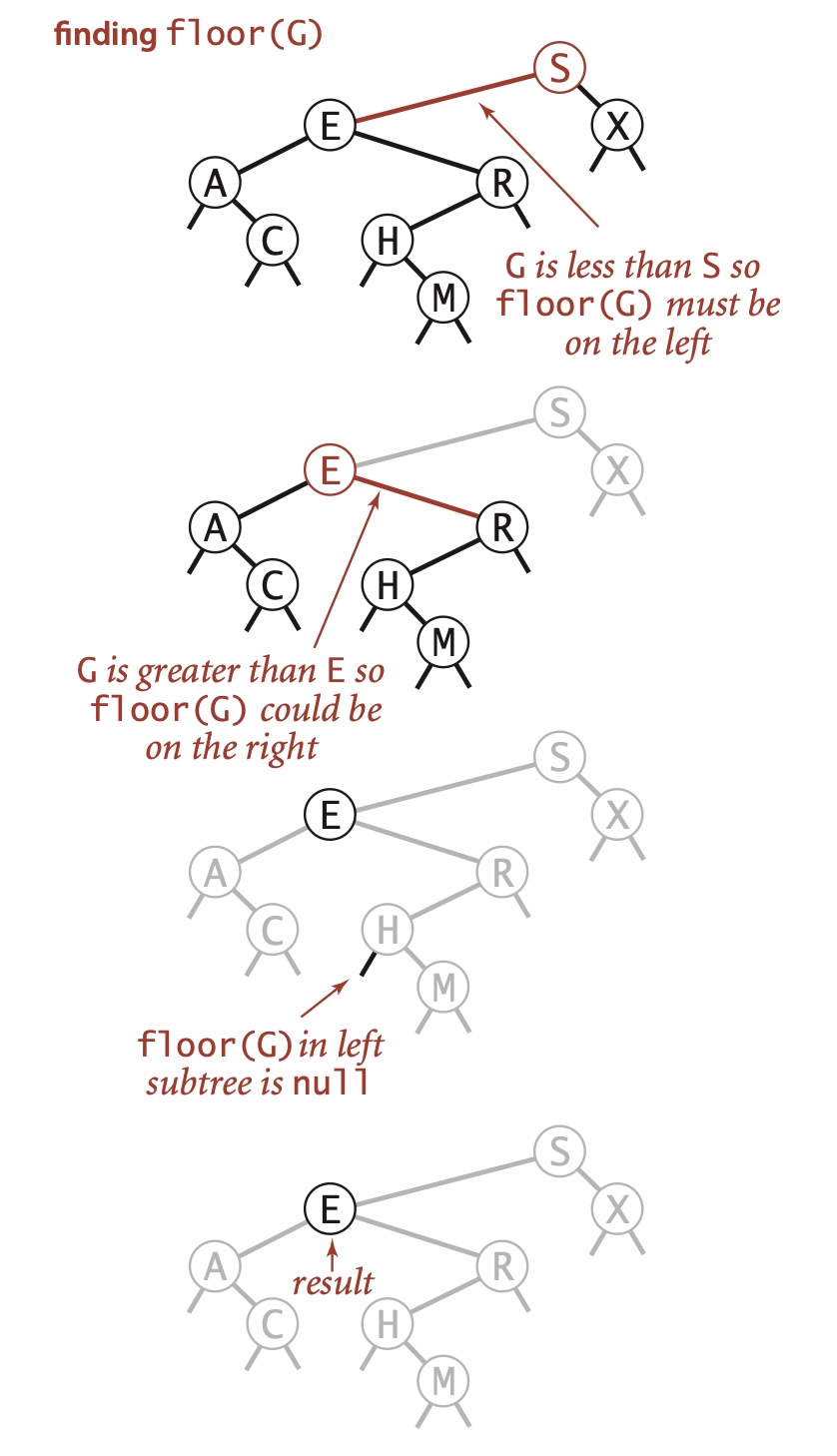
如果给定的键 key 小于二叉查找树的根结点的键,那么小于等于 key 的最大键 floor(key) 一定在根结点的左子树中;如果给定的键key 大于二叉查找树的根结点,那么只有当根结点右子树中存在小于等于 key 的结点时,小于等于 key 的最大键才会出现在右子树中,否则根结点就是小于等于key的最大键。
public class BST<Key extends Comparable<Key>, Value> {
/**
* Returns the largest key in the symbol table less than or equal to {@code key}.
*
* @param key the key
* @return the largest key in the symbol table less than or equal to {@code key}
* @throws NoSuchElementException if there is no such key
* @throws IllegalArgumentException if {@code key} is {@code null}
*/
public Key floor(Key key) {
if (key == null)
throw new IllegalArgumentException("argument to floor() is null");
if (isEmpty())
throw new NoSuchElementException("calls floor() with empty symbol table");
Node x = floor(root, key);
if (x == null)
throw new NoSuchElementException("argument to floor() is too small");
else return x.key;
}
private Node floor(Node x, Key key) {
if (x == null) return null;
int cmp = key.compareTo(x.key);
if (cmp == 0) return x;
if (cmp < 0) return floor(x.left, key);
Node t = floor(x.right, key);
if (t != null) return t;
else return x;
}
/**
* Returns the smallest key in the symbol table greater than or equal to {@code key}.
*
* @param key the key
* @return the smallest key in the symbol table greater than or equal to {@code key}
* @throws NoSuchElementException if there is no such key
* @throws IllegalArgumentException if {@code key} is {@code null}
*/
public Key ceiling(Key key) {
if (key == null)
throw new IllegalArgumentException("argument to ceiling() is null");
if (isEmpty())
throw new NoSuchElementException("calls ceiling() with empty symbol table");
Node x = ceiling(root, key);
if (x == null)
throw new NoSuchElementException("argument to ceiling() is too large");
else return x.key;
}
private Node ceiling(Node x, Key key) {
if (x == null) return null;
int cmp = key.compareTo(x.key);
if (cmp == 0) return x;
if (cmp < 0) {
Node t = ceiling(x.left, key);
if (t != null) return t;
else return x;
}
return ceiling(x.right, key);
}
}2.3 选择操作(select)
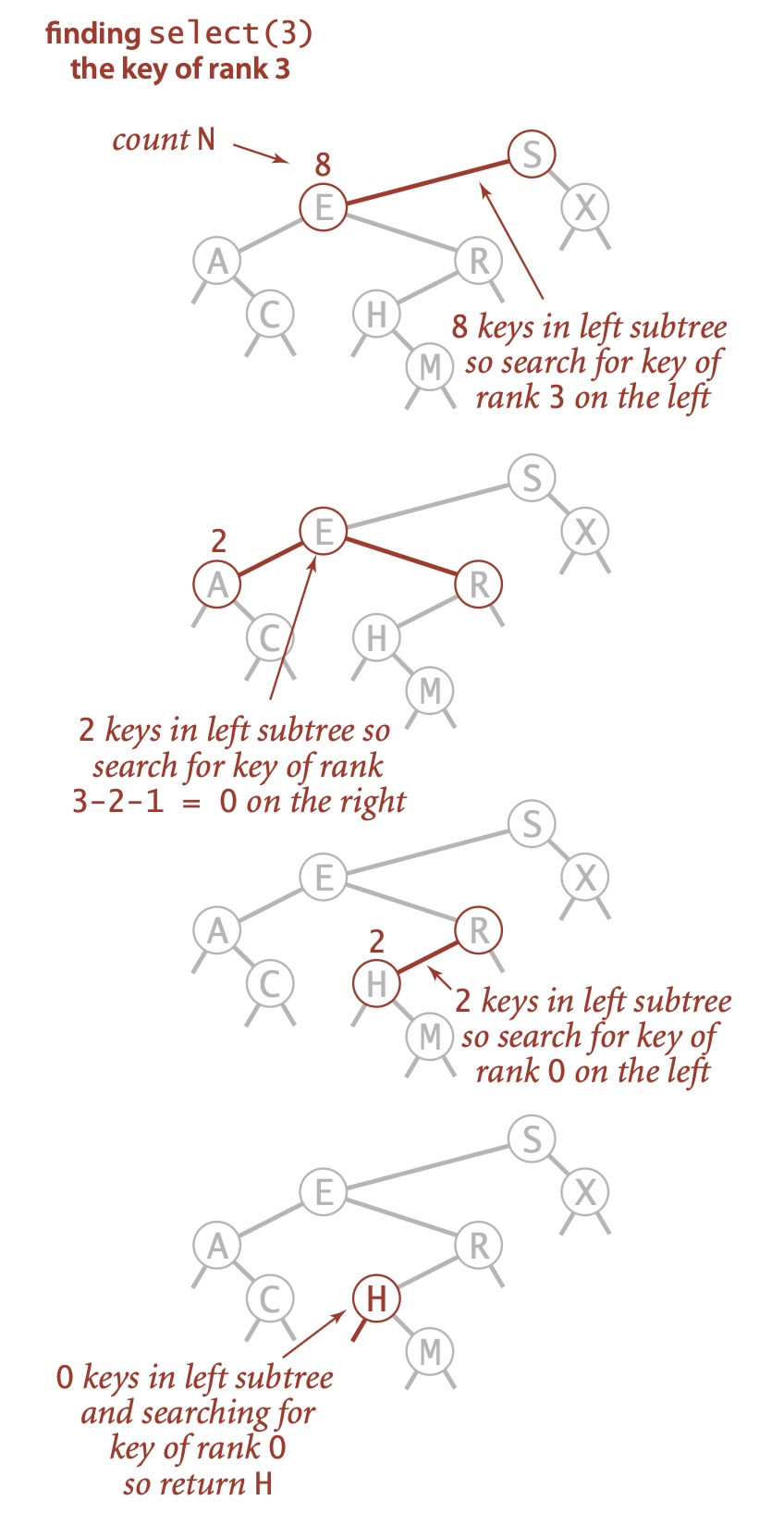
假设我们想找到排名为 k 的键(即树中正好有 k 个小于它的键)。如果左子树中的结点数 t 大于 k 那么我们就继续(递归地)在左子树中查找排名为 k 的键;如果等于 k,我们就返回根结点中的键如果 t 小于 k,我们就(递归地)在右子树中查找排名为 (k-t-1) 的键。
public class BST<Key extends Comparable<Key>, Value> {
/**
* Return the key in the symbol table of a given {@code rank}.
* This key has the property that there are {@code rank} keys in
* the symbol table that are smaller. In other words, this key is the
* ({@code rank}+1)st smallest key in the symbol table.
*
* @param rank the order statistic
* @return the key in the symbol table of given {@code rank}
* @throws IllegalArgumentException unless {@code rank} is between 0 and
* <em>n</em>–1
*/
public Key select(int rank) {
if (rank < 0 || rank >= size()) {
throw new IllegalArgumentException("argument to select() is invalid: " + rank);
}
return select(root, rank);
}
// Return key in BST rooted at x of given rank.
// Precondition: rank is in legal range.
private Key select(Node x, int rank) {
if (x == null) return null;
int leftSize = size(x.left);
if (leftSize > rank) return select(x.left, rank);
else if (leftSize < rank) return select(x.right, rank - leftSize - 1);
else return x.key;
}
}2.4 排名(rank)
rank() 是 select() 的逆方法,它会返回给定键的排名。它的实现和 select() 类似:如果给定的键和根结点的键相等,我们返回左子树中的结点总数 t;如果给定的键小于根结点,我们会返回该键在左子树中的排名(递归计算);如果给定的键大于根结点,我们会返回 t+1 (根结点)加上它在右子树中的排名(递归计算)。
public class BST<Key extends Comparable<Key>, Value> {
/**
* Return the number of keys in the symbol table strictly less than {@code key}.
*
* @param key the key
* @return the number of keys in the symbol table strictly less than {@code key}
* @throws IllegalArgumentException if {@code key} is {@code null}
*/
public int rank(Key key) {
if (key == null)
throw new IllegalArgumentException("argument to rank() is null");
return rank(key, root);
}
// Number of keys in the subtree less than key.
private int rank(Key key, Node x) {
if (x == null) return 0;
int cmp = key.compareTo(x.key);
if (cmp < 0) return rank(key, x.left);
else if (cmp > 0) return 1 + size(x.left) + rank(key, x.right);
else return size(x.left);
}
}2.5 删除最大键(deleteMax)和删除最小键(deleteMin)
二叉查找树中最难实现的方法就是 delete() 方法,我们先考虑 deleteMin() 方法。
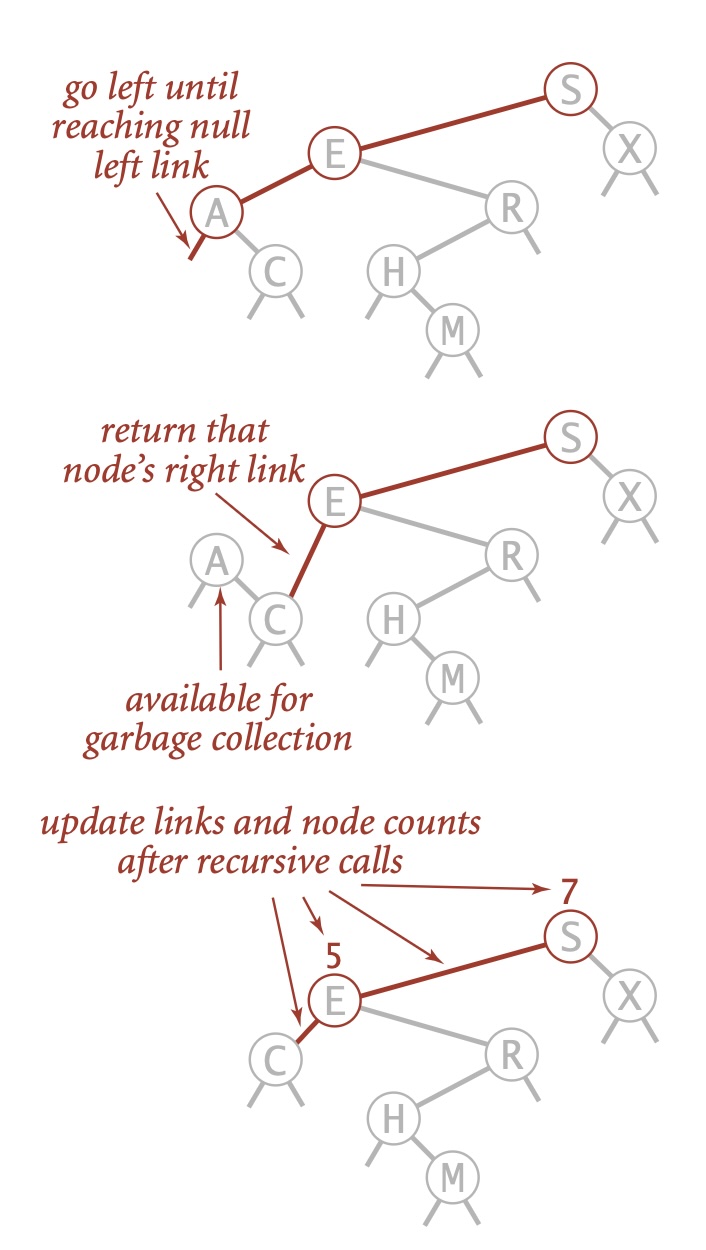
对于 deleteMin(),我们要不断深入根结点的左子树中直至遇见一个空链接,然后将指向该结点的链接指向该结点的右子树(只需要在递归调用中返回它的右链接即可)。最后更新它到根结点的路径上的所有结点的计数器的值。
public class BST<Key extends Comparable<Key>, Value> {
/**
* Removes the smallest key and associated value from the symbol table.
*
* @throws NoSuchElementException if the symbol table is empty
*/
public void deleteMin() {
if (isEmpty()) throw new NoSuchElementException("Symbol table underflow");
root = deleteMin(root);
assert check();
}
private Node deleteMin(Node x) {
if (x.left == null) return x.right;
x.left = deleteMin(x.left);
x.size = size(x.left) + size(x.right) + 1;
return x;
}
/**
* Removes the largest key and associated value from the symbol table.
*
* @throws NoSuchElementException if the symbol table is empty
*/
public void deleteMax() {
if (isEmpty()) throw new NoSuchElementException("Symbol table underflow");
root = deleteMax(root);
assert check();
}
private Node deleteMax(Node x) {
if (x.right == null) return x.left;
x.right = deleteMax(x.right);
x.size = size(x.left) + size(x.right) + 1;
return x;
}
}2.6 删除操作(delete)
我们可以用类似 deleteMax() 和 deleteMin() 的方式删除任意只有一个子结点(或者没有子结点)的结点。
应该怎样处理删除一个拥有两个子结点的结点?删除之后我们要处理两棵子树,但被删除结点的父结点只有一条空出来的链接。
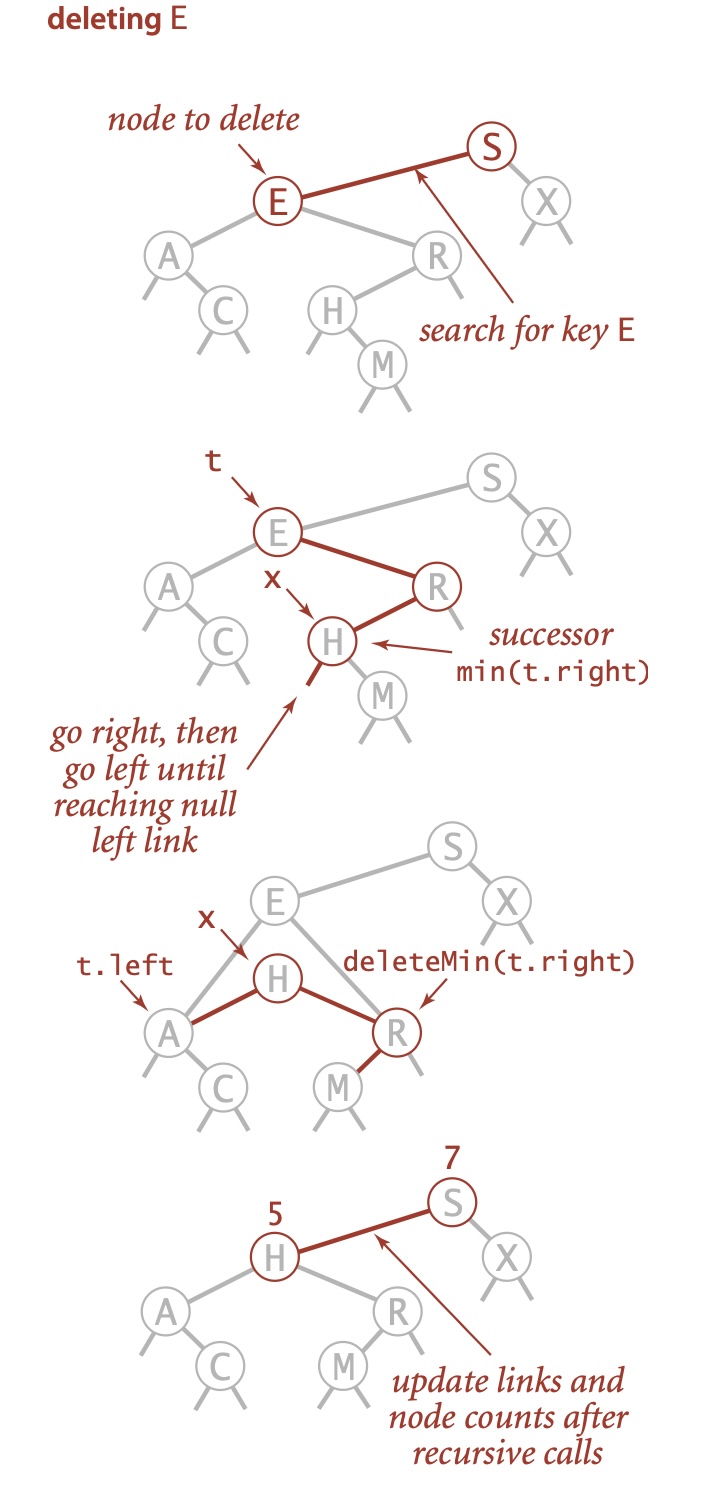
一个方法是,在删除结点 x 后用它的后继结点填补它的位置。因为 x 有一个右子结点,因此它的后继结点就是其右子树中的最小结点。这样的替换仍然能够保证树的有序性,因为 x.key 和它的后继结点的键之间不存在其他的键。我们能够用 4 个简单的步骤完成将 x 替换为它的后继结点的任务:
- 将指向即将被删除的结点的链接保存为 t
- 将 x 指向它的后继结点 min(t.right)
- 将 x 的右链接(原本指向一棵所有结点都大于 x.key 的二叉查找树)指向 deleteMin(t.right),也就是在删除后所有结点仍然都大于 x.key 的子二叉查找树
- 将 x 的左链接(本为空)设为 t.left(其下所有的键都小于被删除的结点和它的后继结点)
public class BST<Key extends Comparable<Key>, Value> {
/**
* Removes the specified key and its associated value from this symbol table
* (if the key is in this symbol table).
*
* @param key the key
* @throws IllegalArgumentException if {@code key} is {@code null}
*/
public void delete(Key key) {
if (key == null)
throw new IllegalArgumentException("calls delete() with a null key");
root = delete(root, key);
assert check();
}
private Node delete(Node x, Key key) {
if (x == null) return null;
int cmp = key.compareTo(x.key);
if (cmp < 0) x.left = delete(x.left, key);
else if (cmp > 0) x.right = delete(x.right, key);
else {
if (x.right == null) return x.left;
if (x.left == null) return x.right;
Node t = x;
x = min(t.right);
x.right = deleteMin(t.right);
x.left = t.left;
}
x.size = size(x.left) + size(x.right) + 1;
return x;
}
}这种法能够正确地删除一个结点,它的一个缺陷是可能会在某些实际应用中产生性能问题。这个问题在于选用后继结点是一个随意的决定,且没有考虑树的对称性。实际上,前趋结点和后继结点的选择应该是随机的。一般情况下这段代码的效率不错,但对于大规模的应用来说可能会有一点问题。
2.7 范围查找(keys)
要实现能够返回给定范围内键的 keys() 方法,我们首先需要一个遍历二叉查找树的基本方法,叫做中序遍历。先打印出根结点的左子树中的所有键,然后打印出根结点的键,最后打印出根结点的右子树中的所有键。
将所有落在给定范围以内的键加入一个队列 Queue 并跳过那些不可能含有所查找键的子树,用例不需要知道我们使用 Queue 来收集符合条件的键。我们使用什么数据结构来实现 Iterable<key> 并不重要,用例只要能够使用 Java 的 foreach 语句遍历返回的有键就可以了。
public class BST<Key extends Comparable<Key>, Value> {
/**
* Returns all keys in the symbol table in ascending order,
* as an {@code Iterable}.
* To iterate over all of the keys in the symbol table named {@code st},
* use the foreach notation: {@code for (Key key : st.keys())}.
*
* @return all keys in the symbol table in ascending order
*/
public Iterable<Key> keys() {
if (isEmpty()) return new Queue<Key>();
return keys(min(), max());
}
/**
* Returns all keys in the symbol table in the given range
* in ascending order, as an {@code Iterable}.
*
* @param lo minimum endpoint
* @param hi maximum endpoint
* @return all keys in the symbol table between {@code lo}
* (inclusive) and {@code hi} (inclusive) in ascending order
* @throws IllegalArgumentException if either {@code lo} or {@code hi}
* is {@code null}
*/
public Iterable<Key> keys(Key lo, Key hi) {
if (lo == null) throw new IllegalArgumentException("first argument to keys() is null");
if (hi == null) throw new IllegalArgumentException("second argument to keys() is null");
Queue<Key> queue = new Queue<Key>();
keys(root, queue, lo, hi);
return queue;
}
private void keys(Node x, Queue<Key> queue, Key lo, Key hi) {
if (x == null) return;
int cmplo = lo.compareTo(x.key);
int cmphi = hi.compareTo(x.key);
if (cmplo < 0) keys(x.left, queue, lo, hi);
if (cmplo <= 0 && cmphi >= 0) queue.enqueue(x.key);
if (cmphi > 0) keys(x.right, queue, lo, hi);
}
}2.8 性能分析
在一棵二叉查找树中,所有操作在最坏情况下所需的时间都和树的高度成正比。